Karthik Mohan

Happy Easter Sunday!🐰

I’m using the time during this long weekend to do some GPU benchmarking. This time, I’m evaluating using raw cuda and numba implementations.

By writing my own implementation, I have more control over the benchmarking process, and this will be an evolving blog.

I am starting off with a roofline model implementation against a variety of kernels. For those unfamiliar with this model, The roofline model wiki page provides a comprehensive explanation.

The preliminary benchmarking I plan to do is against two types of kernels which I am defining as follows:

@cuda.jit
def kernel1(a, b):
    idx = cuda.grid(1)
    stride = cuda.gridsize(1)
    for i in range(idx * 128, a.size - 128, stride * 128):
        for j in range(128):
            val = a[i + j]
            b[i + j] = val * 1.1 + 0.1  

 @cuda.jit
def kernel2(a, b):
    idx = cuda.grid(1)
    if idx < a.size:
        val = a[idx]
        for _ in range(1000):
            val = 0.03 * val + 3 
        b[idx] = val

If you look closely, the compute bound kernel that I am defining is ~2 FLOPS for every iteration of the loop. So, for 1000 iterations, it’s 2000 FLOPS in total. The memory bound kernel defined above is 2 FLOPS per element. I use float32 datatype for for a and b, and this specific kernel requires 2 access per element.

I am first running this benchmark against my newest gpu RTX 4060 Ti which is already loaded in my system.

A few basic stats of this specific gpu,

GPU: NVIDIA GeForce RTX 4060 Ti
Peak Compute Performance: 11.29 TFLOPs/s
Peak Memory Bandwidth: 144.02 GB/s

Results of the above kernels

Memory-bound: 6.88 GB/s, Intensity: 0.2500, Performance: 0.0017 TFLOPs
Compute-bound: Intensity: 250.00, Performance: 0.30 TFLOPs

For the simple kernels I defined above, the results are expected, resulting in the following unoptimized roofline curve. The focus for now is not on optimizing this curve but on ensuring that the roofline model itself is implemented correctly.

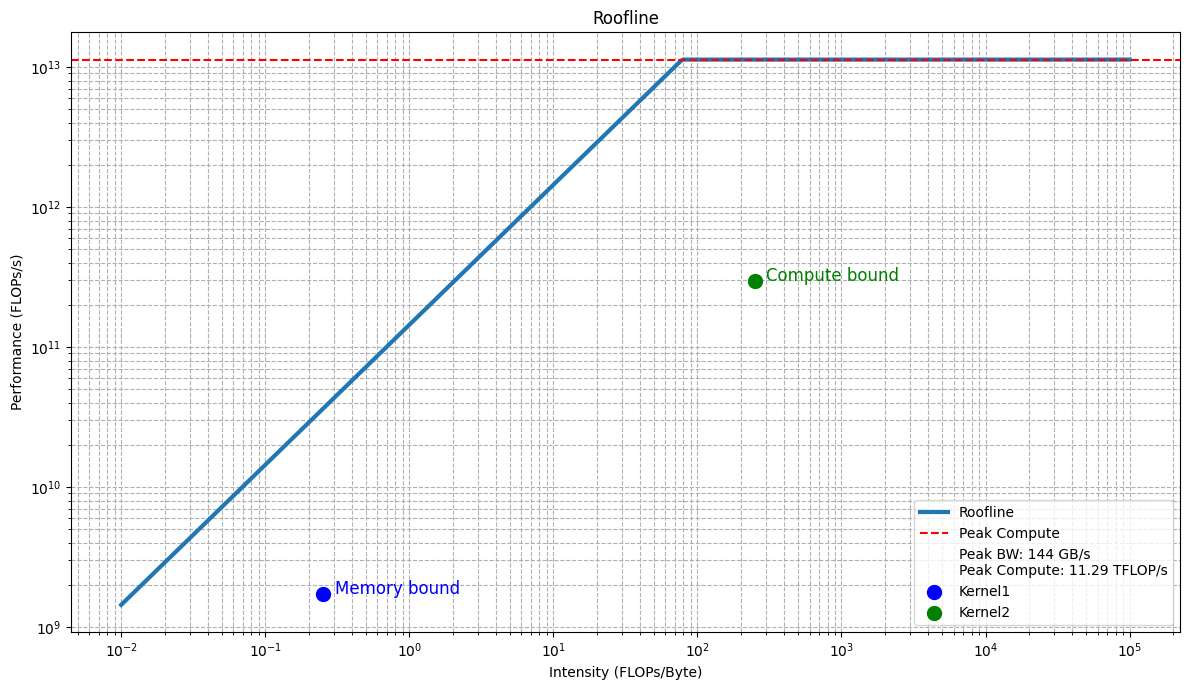
From the results, it’s clear that I now have a clean implementation of a roofline model, which I further plan to expand and use across all my kernel optimization tasks. Pretty Neat, eh! 🤙🏻

I’ll continue to post more updates on this here, so stay tuned!